Inductive Logic Programming - Theory
Inductive inference is, in a sense, the inverse of deduction. However,
deductive inference proceeds by application of sound rules of inference,
while inductive inference typically involves unsound conjecture.
Deductive inference derives consequences E from a prior theory T. Similarly,
inductive inference derives a general belief T from specific beliefs E.
In both deduction and induction T and E must be consistent and
Within ILP it is usual to separate the above elements into examples
(E), background knowledge (B), and hypothesis (H). These have the relationship
B, H and E are each logic programs. E usually consists of ground unit
clauses of a single target predicate. E can be separated into positive
examples (E+), as ground unit definite clauses and negative examples (E-),
ground unit headless Horn clauses. However, the separation into B, H and
E is a matter of convenience
Inverse Resolution
Logic Programming relies heavily on Robinson's seminal work on Resolution
Theorem Proving. He demonstrated that deductive inference in the first
order predicate calculus could be effected by the single Resolution rule
of inference. This forms a basis for the programming system Prolog.
A single resolution step is shown below
Inductive inference based on inverting resolution in propositional logic
was the basis of the inductive inference rules within the Duce
system. Duce had six inductive inference rules. Four of these were
concerned with definite clause propositional logic. In the following description
of the inference rules lower-case letters represent propositional variables
and upper-case letters represent conjunctions of propositional variables.
Duce's inference rules invert single-depth applications of resolution.
Using the rules a set of resolution-based trees for deriving the examples
can be constructed backwards from their roots. The set of leaves of the
trees represent a theory from which the examples can be derived. In the
process new proposition symbols, not found in the examples, can be ''invented''
by the intra- and inter-construction rules.
Inverse Resolution
in First Order Logic
Inverse resolution was lifted to first-order predicate calculus. This involved
algebraic inversion of the equations of resolution below.
Figure 1 shows a resolution step. During a deductive resolution step
D is derived at the base of the 'V' given the clauses on the arms. In contrast,
a 'V' inductive inference step derives one of the clauses on the arm of
the `V' given the clause on the other arm and the clause at the base. In
Figure 1 the literal resolved is positive (+) in C and negative (-) in
C'. Duce's absorption rule constructs C' from C and D, while the identification
rule derives C from C' and D.
Since algebraic inversion of resolution has a complex non-deterministic
solution only a restricted form of absorption was implemented in Cigol
(logiC backwards). However, there is a unique most-specific solution for
`V' inductive inference rules. That is
where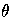 
is such
that 
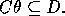Rather than inverting the equations of resolution we might consider resolution
from the model-theoretic point of view. That is
Applying the deduction theorem gives a deductive solution for absorption.
This is a special case of inverting implication.
Relative Least General Generalisation (rlgg)
One commonly advocated approach to learning from positive data is that
of taking relative least general generalisations (rlggs) of clauses.
In the late 1960s Reynolds and Plotkin investigated the problem of finding
least general generalisations (lggs) of atoms. The work focused on the
importance of Robinson's unification to deduction, and searched for an
analogue useful in induction. Lggs were found to be, in some sense, an
inverse to unification.
Plotkin extended the investigation to clauses. He then went on to define
the lgg of two clauses relative to clausal background knowledge B.
Assume that one is attempting to learn target concept T, from examples
E={x_1,x_2,...,x_m}. Given background knowledge , H=rlgg_B (E) will be
the hypothesis within the relative subsumption lattice with the fewest
possible errors of commission (instances x in X for which H entails x and
T does not entail x).
This approach to learning from positive data has the following problems.
-
Arbitrary background knowledge. Plotkin showed that with unrestricted definite
clause background knowledge B there may not be any finite rlgg_B(E).
-
Extensional background knowledge. Suppose B and E consist of n and m ground
unit clauses respectively. In the worst case the number of literals in
rlgg_B(E) will be (n+1)^m, making the construction intractable for large
m.
-
Multiple clause hypothesis. Target concepts with multiple clauses cannot
be learned since rlgg_B(E) is a single clause.
The ILP system Golem
was designed to learn by creating rlggs. Golem used extensional background
knowledge to avoid the problem of non-finite rlggs. Extensional background
knowledge B can be generated from intensional background knowledge B' by
generating all ground unit clauses derivable from B' in at most h resolution
steps. The parameter h is provided by the user. The rlggs constructed by
Golem were forced to have only a tractable number of literals by requiring
that the set of possible hypotheses contain only definite clause theories
that were ij-determinate.
Inverse Implication (II)
The inability to invert implication between clauses limits the completeness
of inverse resolution and rlggs since θ-subsumption
is used in place of clause implication in both. Plotkin noted that if clause
C θ-subsumes clause
D (or Cθ ⊆ D.)
then C -> D. However, he also notes that C -> D does not imply Cθ ⊆ D.
Although efficient methods are known for enumerating every clause C which θ-subsumes
an arbitrary clause D, this is not the case for clauses C which imply D.
This is known as the problem of inverting implication between clauses.
Gottlob proved a number of properties concerning implication between
clauses. He demonstrated that for any two non-tautological clauses, C,D,
where C+, C-, and D+, D- be the sets of positive and negative literals
of clauses C and D respectively, then C -> D implies that C+ θ-subsumes
D+ and C- θ-subsumes
D-.
Sub-unification has been applied In an attempt to solve the inverting
implication problem. Sub-unification is a process of matching sub-terms
in D to produce C. It has been demonstrated that sub-unification is able
to construct recursive clauses from fewer examples than would be required
by ILP systems such as Golem and FOIL.
Another notable Lemma was proved by Lee. This states that a clause T
implies clause C if and only if there exists a clause D in the resolution
closure of T, such that θ-subsumes
C.
In particular it is shown that Lee's subsumption lemma has the following
corollary. (Implication and recursion)
Let C, D be clauses. C -> D if and only if either D is a tautology or
C θ-subsumes D
or there is a clause E such that E θ-subsumes
D where E is constructed by repeatedly self-resolving C.
Thus the difference between θ-subsumption
and implication between clauses C and D is only pertinent when C can self-resolve.
Attempts were made to a) extend inverse resolution and b) use a mixture
of inverse resolution and lgg to solve the problem. The extended inverse
resolution method suffers from problems of non-determinacy. Idestam-Almquist's
use of lgg suffers from the standard problem of intractably large clauses.
Both approaches are incomplete for inverting implication, though Idestam-Almquist's
technique is complete for a restricted form of entailment called T-implication.
It has been shown that for certain recursive clauses D, all the clauses
C which imply D also θ-subsume
a logically equivalent clause D'. Up to renaming of variables every clause
D has at most one most specific form of D' in the θ-subsumption
lattice. D' is called the self-saturation of D. However, there exist definite
clauses which have no finite self-saturation.
Inverse Entailment (IE)
The general problem specification of ILP is, given background knowledge
B and examples E find the simplest consistent hypothesis H (where simplicity
is measured relative to a prior distribution) such that
Note, in general B, H and E could be arbitrary logic programs. Each
clause in the simplest H should explain at least one example, since otherwise
there is a simpler H' which will do. Consider then the case of H and E
each being single Horn clauses. This can now be seen as a generalised form
of absorption and rearranged similarly to give
Since H and E are each single clauses, their negation will be logic
programs consisting only of ground skolemised unit clauses. Let
be the (potentially infinite) conjunction of ground literals which are
true in all models of 
.
Since 
must be true in
every model of
it must contain a subset of the ground literals in .
Therefore
and so for all H
A subset of the solutions for H can be found by considering the clauses
which 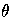-subsume 
.
The complete set of candidates for H can be found by considering all clauses
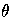which -subsume
sub-saturants of .
U-Learnability is a new model of learnability, and is an alternative to
PAC-Learnability. U-Learnability better matches the practical goals of
machine learning.
The major features of U-learnability that distinguishes it from PAC-learnability
are:
-
The use of probability distributions over concept classes, which assign
probabilities to potential target concepts.
-
Average-case sample complexity and time complexity requirements, rather
than worst-case requirements.
In the U-learnabilty model, a teacher randomly chooses a target concept
according to a probability distribution over the concept class. The teacher
then chooses examples randomly, with replacement, according to a probability
distribution over the domain of examples, and labels the examples according
to the chosen target. In general, these distributions may be known, completely
unknown, or partially known to the learner. In the case where these distributions
are completely unknown, then worst case analysis must be used as in PAC-learnability.
More formally, the teacher starts by choosing distributions F and G
from the family of distributions over concept descriptions H (wffs with
associated bounds for time taken to test entailment) and instances X (ground
wffs) respectively. The teacher uses F and G to carry out an infinite series
of teaching sessions. In each session a target theory T is chosen from
F. Each T is used to provide labels from (True, False) for a set of instances
randomly chosen according to distribution G. The teacher labels each instance
x_i in the series < x_1, .., x_m > with True if T entails x_i and False
otherwise. An hypothesis H is said to explain a set of examples E whenever
it both entails and is consistent with E. On the basis of the series of
labelled instances < e_1, e_2, ..., e_m >, a Turing machine learner
L produces a sequence of hypotheses < H_1, H_2, ... H_m > such that
H_i explains { e_1, ..., e_i }. H_i must be suggested by L in expected
time bounded by a fixed polynomial function of i. The teacher stops a session
once the learner suggests hypothesis H_m with expected error less than
e for the label of any x_m+1 chosen randomly from G. < F, G > is said
to be U-learnable if and only if there exists a Turing machine learner
L such that for any choice of d and e (0 < d, e =< 1) with probability
at least (1-d) in any of the sessions m is less than a fixed polynomial
function of 1/d and 1/e.
The figure below shows the effect E={e1,.., em} has on the probabilities
associated with the possible hypotheses.
U-leanability may be interpreted from a Bayesian perspective. The figure
shows the effect of a series of examples on the probabilites associated
with hypotheses. The learner's hypothesis language is laid out along the
X-axis with prior probability p(H) = F(H) for a H taken from the set of
all hypotheses measured along the Y-axis, where the sum of all probabilites
of the hypotheses is 1.
The descending dotted line in the Figure represents a bound on the prior
probabilities of hypotheses before consideration of examples E. The hypotheses
which entail and are consistent with the examples are marked as vertical
bars. The prior probability of E, p(E), is simply the sum of probabilities
of hypotheses in that explain the examples. The conditional probability
p(E|H) is 1 in the case that H explains E and 0 otherwise. The posterior
probability of H is now given by Bayes theorem as
For an hypotheses H which explains all the data, p(H|E) will increase
monotonically with increasing E.
U-learnability has demonstrated positive results for the popular decision
tree learning program, CART.
Research Issues
This section provides a breif outline of the reseach areas that will extend
current ILP theory and systems.
Background Knowledge.
-
Relevance. When large numbers of background predicates are available, determining
which predicate is relevant.
-
Revision. How clauses should be removed, or unfolded with respect to deep-structured
theories.
-
Invention. Further research is required into predicate invention.
Complex Theories.
-
Multi-clause. Most present ILP systems are concerned with generating a
single clause. Research is required into improved performance of multiple
clause generation.
-
Deep Theories. Current ILP systems perform poorly in the presence of relevant
long chains of literals, connected by shared variables.
-
Recursion. Recursive hypotheses are poorly handled by most ILP system.
This is particularly important in the natural language domain.
-
Structure. Structural concepts result in complex clauses when encoded as
literals. These present problems to the search strategies used in current
ILP systems.
Built-in semantics.
-
Numbers. ILP systems have severe restrictions on the form of numeric constraints
that can be used.
-
Probabilities. ILP systems lack the ability te express probabilistic constraints.
This effects the performance of ILP systems in the database discovery domain.
-
Constraints. ILP system require the ability to learn and make use of general
constraints, rather than requiring large numbers of ground negative examples.
-
Built-in predicates. Some predicates are best defined procedurally. ILP
systems may experience improved efficiency of learning using built-in predicates.
Sampling Issues.
-
Large Data Sets. Incremental learning systems may be more effective than
batch systems, where difficulties are experienced with learning from all
examples at once.
-
Small Data Sets. Statistical tests for significance break down when learning
from small data sets. ILP systems need to demonstrate high predictive accuracy
with samll training sets.
-
Reliability. Extending ILP systems to indicate reliability estimates when
exact generalisations are not possible.
Machine
Learning at the Computing Lab